I strongly identified with the work of Peter Liljedahl as it immediately struck me as the type of learners, I want my students to be, motivated, curious, self-directed thinkers. It also reminded me of the work of the Critical Thinking Consortium whose ideas I was exposed to as an education student at UBC and have informed my practice in science and social studies. We teach students to be deep and purposeful thinkers in language arts though the work of Adrienne Gear and Reading and Writing Power and build our thinking skills for historical and geographic thinking in social studies, even the scientific method builds thinking skills. However, this has been lacking in much of our math education, I know as a student myself I was not encouraged to think even in university calculus, I was to apply the rules, follow the formula and just use the algorithm. This doesn’t build curious mathematicians or students who want to engage with math. By making math about applying a formula with no reason why we have the formula to begin with we rob students of the joy of math. We have outcomes in language arts that state “Language and text can be a source of creativity and joy.” (British Columbia Ministry of Education, 2020) yet there is nothing in the math curriculum that has a comparable big idea. In A Mathematicians Lament Lockhart draws a comparison to teaching students to paint by only ever giving them lessons on the materials and the skill, having them paint by numbers but never allowing students the opportunity to openly create and to discover their own sense of wonder and creativity (Lockhart, 2002). Many math programs deny students the beauty of math by using repetitive worksheets with limited or no problem solving and removing opportunity for students to explore math.
The Critical Thinking Consortium a British Columbia based group of educators that advocates for teaching students to be critical, creative, and collaborative thinkers has released information on what they call powerful math that aligns with Liiljedahl’s Building Thinking classrooms. The goal of both is to get students thinking and engaging with math in ways that are purposeful and meaningful to the student. Both encourage the use of problem solving and critical inquiry into a problem. They are focused on the same end goal, students who can think mathematically and enjoy thinking mathematically.
Thinking skills across disciplines.
| Reading Powers | Scientific Method | Historical Thinking | Geographic Thinking |
| Connect Question Visualize Infer Transform Zoom in | Observe Question Predict Hypothesize Test Check | Significance Evidence Continuity and change Cause and consequence Perspective Ethical judgement | Significance Patterns and trends Connections and interrelationships Perspective (ESRI, n.d.) 5 Themes of Geography Place, Space, Location, Region, Human Environment Interaction |
Many of the ideas presented by Liljedahl correspond with these concepts fit the needs of learns for thinking across disciplines. All the disciplines listed have an element of questioning, making connections and visualizing. This consistency of skills across all disciplines could be extended to math as was demonstrated by Liljedahl in various publications. By promoting thinking in math class, we allow students to experience the joy and wonder, the beautiful simplicity of math discussed by Lockhart. Students need to think mathematically to be numerate in our world and to be able to adapt as the world changes, we will always be able to google a formula, but we can’t google thinking.
As teachers it is our goal to help students become independent lifelong thinkers. The work presented by Liljedahl and the Critical Thinking Consortium promotes student thinking. It is not enough in our world to simply know a times table or to have memorized a formula. In recent weeks we have been working on some renovations including discussing new flooring, while I know the formula for the area of a rectangle only one room in my house is a regular rectangle, I had to have the skills to think mathematically and draw out the plan with measurements for each room before portioning the rooms into regular rectangles to calculate the area. Yes, I used the standard formula to calculate the area of each smaller rectangle, but I had to think mathematically to determine my rectangles or to even know where to start drawing my diagram. Drawing a diagram or a graph is a skill we encourage in math to help students understand the problem and it connects directly to the concept of visualizing taught in other content areas. A manipulative takes the concept of visualization further to a real or symbolic object. We could spend weeks or months teaching students to visualize math the same way we spend time teaching them to visualize in language arts. If we want our students to be confident, lifelong mathematical thinkers we must take the time to teach them the thinking skills needed.
Liiljedahl’s approach was contrasted in the debate with Jump math which I had some initial curiosity about then after viewing the samples understand why my district recommends that it not be used. The pages I viewed from the samples appeared to have a lot of rote computation and little actual thinking for students, it emphasized an algorithm or specific skill with numerous practice problems. While this might be a good review or support for a few students many students would find this to monotonous. Work like what I saw on the Jump math site fits the description of math education by Lockhart, that it is killing the joy and the beauty of math. This approach is very teacher centric where the teacher is the sole giver of knowledge this does not presume or promote competence or creativity. The baby steps approach may be positive for some students and may be helpful for students requiring a lot of intervention for basic skills. The program promotes itself as structured inquiry yet when reading their site, I found no evidence of true inquiry that allowed students to formulate their own questions and hypothesise to investigate.
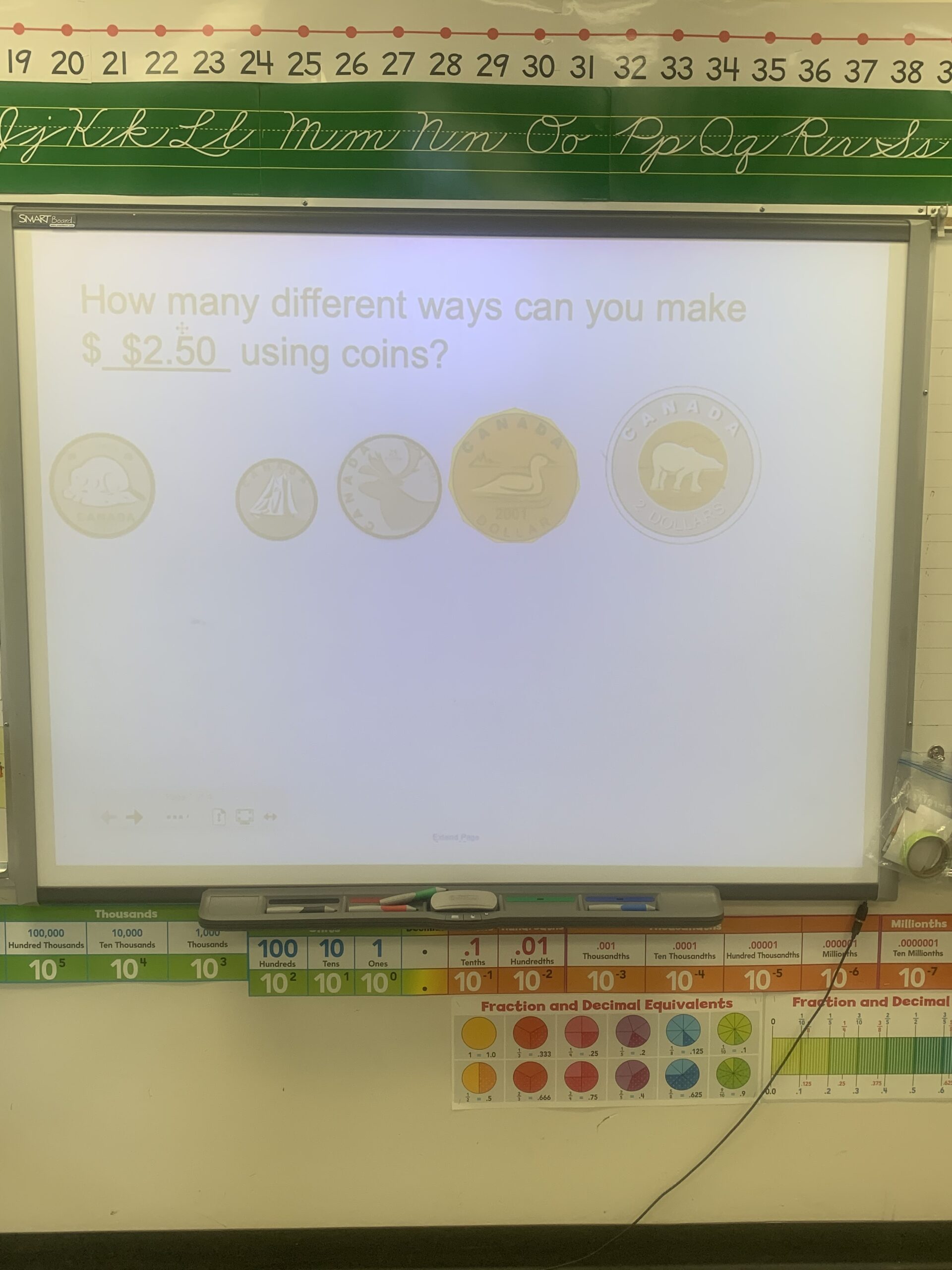
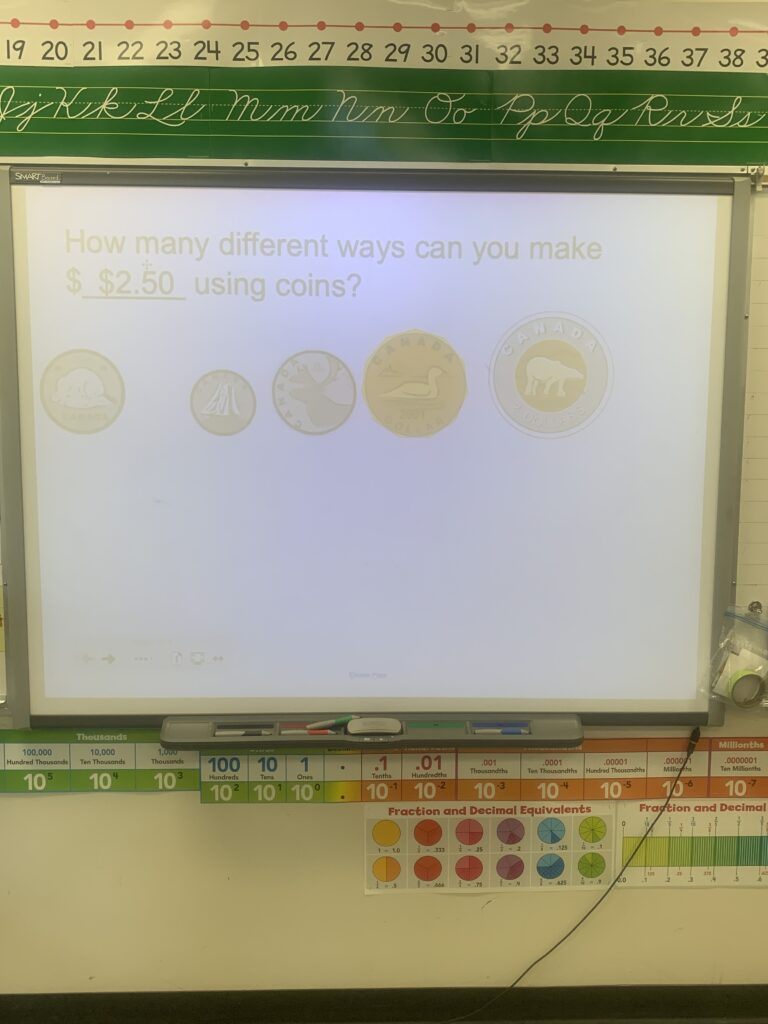
For the past month I have slowly been incorporating these ideas with a huge amount of success, more than I initially expected. While the success is not being reflected in test scores yet I am seeing success in other ways that make me very proud of my class. My students look forward to “math on the wall” and solving “big problems” together. I’ve really noticed a change in the conversations my students are having they are listening to each other more and trying more strategies. The questions they are asking me are also changing I’m hearing less “is this right” and more “what can we do next”. My student’s enthusiasm for math has been the4 greatest success in all of this. My most reluctant mathematician now rushes for the pen and to her white board and cheers if she gets to work on a window, this is a student that in September math brought to tears, in March she was hesitant, now in June she is excited, I really think that the Building Thinking Classrooms approach is working for her. We are starting our math classes with something that every student can engage with and looks forward to, this is increasing our perseverance in math and my students are better able to discuss their understanding of the concepts and how concepts connect to each other. Our number talks and math discussions are much richer now, students are sticking with practice problems longer and are feeling more successful. When looking at their work through formative assessments, most of my students are on track and understanding the concepts. This is something I plan to stick with next year and am looking froward to seeing how our understanding grows when this goes from an end of the year ( Mid May and June) trial to a whole year plan. My initial thoughts are very positive and I can’t wait to see what happens next and where this takes us.
Videos and pod casts
I ended up getting very excited about Building Thinking Classrooms and going down quite the rabbit hole this weekend in figuring out how to present my observations, understanding and opinion.
- Podcasts
- Sum of It All Thinking Classrooms https://open.spotify.com/episode/7HP5tzSdZcYvMMyACwLi7k
- Make Math Moments Episode 21 https://makemathmoments.com/episode21/
- Make Math Moments Episode 98 https://makemathmoments.com/episode98/
- YouTube
Bibliography
British Columbia Ministry of Education. (2020). Grade 4 English Language Arts. Retrieved from Building Student Success: https://curriculum.gov.bc.ca/curriculum/english-language-arts/4/core
ESRI. (n.d.). The Concepts of Geographic Thinking. Retrieved from ESRI Canada: https://www.arcgis.com/apps/MapSeries/index.html?appid=19daf0d08b294e2fb38de3980613e03e
Gini-Newman, L. (2021). A Math Pedagogy designed to empower learners. Retrieved from The Critical Thinking Consortium: https://tc2.ca/uploads/PDFs/25nextsteps/tc2_math_pedagogy.pdf
Liljedahl, P. (2016). Building Thinking Classrooms: Conditions for Problem Solving. In J. Carrillo, & J. Cruz, Posing and Solving Mathematical Problems. Springer.
Liljedahl, P. (2017, October 7). Building a Thinking Classroom in Math. Retrieved from Edutopia: https://www.edutopia.org/article/building-thinking-classroom-math
Liljedahl, P. (2019, April 22). Making Math Moments Matter Episode #21. Making Math Moments Matter. (J. Orr, Interviewer) Making Math Moments Matter.
Liljedahl, P. (2020). 14 Practices. Retrieved from Building Thinking Classrooms: https://buildingthinkingclassrooms.com/14-practices/
Liljedahl, P. (2020). Building Thinking Classrooms. Corwin.
Liljedhal, P. (2021, May 01). #98: The Thinking Classroom Part 2: An interview with Peter Liljedahl. Making Math Moments that Matter. (J. Orr, Interviewer)
Lockhart, P. (2002). A Mathaematician’s Lament.
The Critical Thinking Consortium. (2020). Critical Thinking in Elementary Mathematics: What? Why? When? and How? Retrieved from The Critical Thinking Consortium: https://tc2.ca/uploads/PDFs/25nextsteps/CT_elementary_math.pdf